a×1≅aa×1≅aa \times \mathbf 1 \cong a en categorías que admiten productos y tienen un objeto terminal 11\mathbf 1

Question

a×1≅aa×1≅aa \times \mathbf 1 \cong a en categorías que admiten productos y tienen un objeto terminal 11\mathbf 1

Matemáticas
teoría de categorías
persiguiendo diagramas
solución-verificación

0xd34df00d

Estoy practicando mis habilidades de búsqueda de diagramas y razonamiento y, como ejercicio, estoy tratando de probar que si una categoría tiene productos y también tiene un objeto terminal $\mathbf 1$ , entonces para cualquier $a$ un objeto de la categoría, $a \times \mathbf 1 \cong a$ (Ese también es el ejercicio III.8.4 en "Topoi" de Goldblatt). También estoy tratando de hacer eso rigurosamente sin dejar ningún paso "obvio".

Así que considere este diagrama: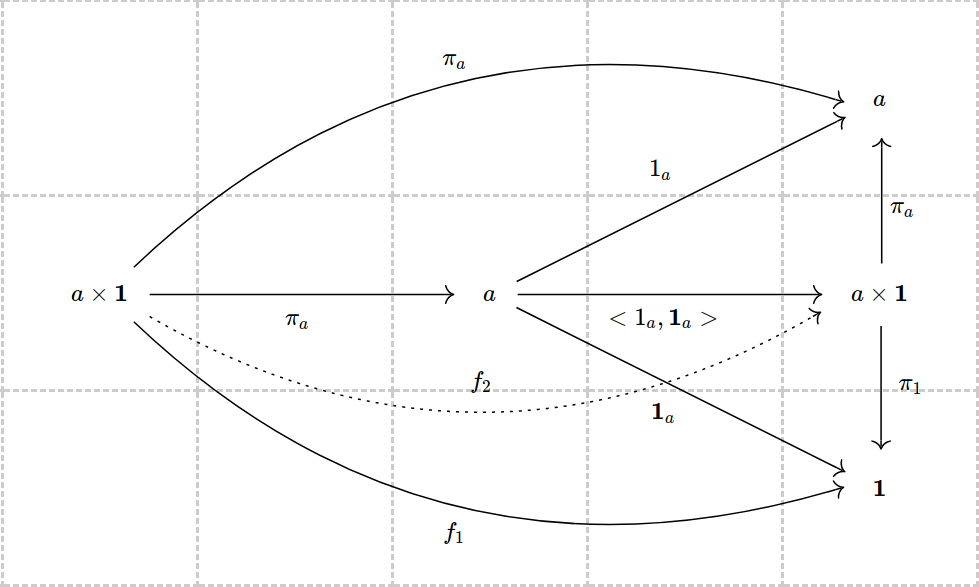

Aquí, $f_1$ y $f_2$ son algunos morfismos de los que no tenemos información previa, se determinarán más adelante.

Primero considere la mitad derecha (comenzando con $a$ ). $<1_a, \mathbf 1_a>$ existe y hace que la mitad derecha viaje por definición del producto. En particular, $1_a = \pi_a \circ <1_a, \mathbf 1_a>$ .

Ahora tenemos que demostrar que $1_{a \times \mathbf 1} = <1_a, \mathbf 1_a> \circ \pi_a$ , y esto es más interesante. Dibujemos $a \times \mathbf 1$ a la izquierda de $a$ junto con los morfismos como en el diagrama.

El triángulo superior izquierdo que acabamos de formar viaja porque $\pi_a = 1_a \circ \pi_a$ por definición de $1_a$ . Esto también implica que todo el triángulo recto superior conmuta (*).

Echemos $f_1$ ser algo que hace que el triángulo inferior izquierdo conmute: $\mathbf 1_a \circ \pi_a$ servirá. Esto también implica que todo el triángulo recto inferior conmuta (**).

A continuación, desde $\mathbf 1$ es terminal, $f_1$ en realidad se ve obligado a ser $\pi_{\mathbf 1}$ , y esto significa que tomando $f_2 = 1_{a \times \mathbf 1}$ hace que el diagrama conmute. Por otro lado, $<1_a, \mathbf 1_a> \circ \pi_a$ también hace conmutar el diagrama, que sigue de (*) y (**). Pero esto significa precisamente que $1_{a \times \mathbf 1} = <1_a, \mathbf 1_a> \circ \pi_a$ , según sea necesario.

¿Parece razonable? ¿Puedo hacerlo mejor?

dave

Es

1_{a}

$1_a$ el mapa de identidad en

a

$a$ ? Si es así, ¿cómo es

1_{a}

$1_a$ un mapa

a \to 1

$a\to 1$ ?

0xd34df00d

@Dave lo siento por el abuso de notación.

1_{a}

$1_a$ es el mapa de identidad de hecho para el objeto

a

$a$ , pero

1_{a}

$\mathbf 1_a$ (observe la fuente en negrita) es el morfismo (único) de

a

$a$ al objeto terminal

1

$\mathbf 1$ .

dave

Oh, bastante justo. No noté la diferencia al principio.

0xd34df00d

Debería haber usado símbolos menos confusos. ¿Cuál es la notación común para este morfismo único?

dave

No conozco una notación común para eso. Aunque normalmente uso

{id}_{a}

$\operatorname{id}_a$ por la identidad en

a

$a$ .

diracdeltafunk

Estoy de acuerdo con @Dave, la mejor manera de evitar una notación confusa en la prueba es escribir

{id}_{a}

$\operatorname{id}_a$ para el mapa de identidad y

1_{a}

$\mathbf{1}_a$ para el mapa único al objeto terminal.

Eric M Schmidt

Una forma más sencilla de probar esto es mostrar directamente que

a

$a$ tiene la propiedad universal de

a \times 1

$a \times \mathbf{1}$ .

Respuestas (1)

a×1≅aa×1≅aa \times \mathbf 1 \cong a en categorías que admiten productos y tienen un objeto terminal 11\mathbf 1

Es $1_a$ el mapa de identidad en $a$ ? Si es así, ¿cómo es $1_a$ un mapa $a\to 1$ ?
@Dave lo siento por el abuso de notación. $1_a$ es el mapa de identidad de hecho para el objeto $a$ , pero $\mathbf 1_a$ (observe la fuente en negrita) es el morfismo (único) de $a$ al objeto terminal $\mathbf 1$ .
Debería haber usado símbolos menos confusos. ¿Cuál es la notación común para este morfismo único?
No conozco una notación común para eso. Aunque normalmente uso $\operatorname{id}_a$ por la identidad en $a$ .
Estoy de acuerdo con @Dave, la mejor manera de evitar una notación confusa en la prueba es escribir $\operatorname{id}_a$ para el mapa de identidad y $\mathbf{1}_a$ para el mapa único al objeto terminal.
Una forma más sencilla de probar esto es mostrar directamente que $a$ tiene la propiedad universal de $a \times \mathbf{1}$ .

diracdeltafunk · Answer 1

Este es un pequeño detalle, pero dado que hay una opción única de $f_1$ , $f_2$ lo que hace que el diagrama conmute, no creo que sea prudente decir " $f_1$ y $f_2$ son algunos morfismos de los que no tenemos información previa, se determinarán más adelante". Es mejor decirle al lector $f_1 = \mathbf{1}_a \circ \pi_a$ y $f_2 = \langle{1_a, \mathbf{1}_a}\rangle \circ \pi_a$ , ya que tenemos suficiente información previa para concluir esto si queremos que el diagrama conmute. Sin embargo, esa es solo mi opinión sobre el estilo de prueba, y no dude en ignorarlo.

Esto lleva a una discusión sobre el único pequeño error en su prueba. Dices "tomando $f_2 = 1_{a \times \mathbf{1}}$ hace que el diagrama conmute", pero solo puede concluir esto si ya sabe que $1_{a \times \mathbf{1}} = \langle 1_a, \mathbf{1}_a \rangle \circ \pi_a$ ! La razón de esto es que por supuesto $1_{a \times \mathbf{1}} = \langle 1_a, \mathbf{1}_a \rangle \circ \pi_a$ debe cumplirse si el diagrama conmuta, y la composición $\langle 1_a, \mathbf{1}_a \rangle \circ \pi_a$ no puede escribirse como una composición diferente de mapas en el diagrama (en particular, $\pi_a$ es la única flecha entrante a $a$ y $\langle{1_a, \mathbf{1}_a}\rangle$ es la única flecha entrante a $a \times \mathbf{1}$ ).

Sin embargo, estás en el camino correcto aquí. Debes hacer explícita la prueba de que $1_{a \times \mathbf{1}} = \langle 1_a, \mathbf{1}_a \rangle \circ \pi_a$ usando el hecho de que $1_{a \times \mathbf{1}} = \langle{\pi_a, \pi_{\mathbf{1}}}\rangle = \langle{\pi_a, f_1}\rangle$ . ¡Espero que esto ayude!

Sabía que omití algo, ¡gracias! De hecho, parece que es mejor considerar un diagrama separado que consiste solo en $a \times \mathbf 1$ como el producto junto con $a \times \mathbf 1$ como algo que se mapea en $a$ y $\mathbf 1$ con $\pi_a$ y $\pi_1$ respectivamente. Entonces el resultado sigue más claramente.
@ 0xd34df00d ¿Me estoy perdiendo algo aquí? ¿No se sigue eso? $1_{a \times \mathbf{1}} = \langle 1_a, \mathbf{1}_a \rangle \circ \pi_a$ simplemente porque hay una flecha única $a \times \mathbf 1 \to a \times \mathbf 1$ (a saber, la identidad) que permite $a \times \mathbf 1$ factorizar a través de sí mismo, por así decirlo?

a×1≅aa×1≅aa \times \mathbf 1 \cong a en categorías que admiten productos y tienen un objeto terminal 11\mathbf 1

0xd34df00d

dave

0xd34df00d

dave

0xd34df00d

dave

diracdeltafunk

Eric M Schmidt

Respuestas (1)

diracdeltafunk

0xd34df00d

gf.c

Los productos triples son isomorfos

¿Los funtores en categorías tipo conjunto conservan inyecciones y sobreyecciones?

Cinco lemas cortos y un contraejemplo: diagrama conmutativo

Crear una nueva categoría que sea el 'opuesto' de una categoría existente (Ej 3.1 de Aluffi Capítulo 0)

Buscando la guía del estudiante para perseguir diagramas

¿Consecuencia del lema cinco o cuatro?

Propiedades básicas de los objetos terminales

Haces de fibras con morfismos de categoría como fibras

K-topología satisface el axioma de Hausdorff

Demostrar que toda subsucesión de una sucesión real convergente converge en el mismo límite.